【Java学习|黑马笔记|Day19】方法引用、异常(try...catch、自定义异常)及其练习
【Java学习|黑马笔记|Day19】
今天看的是黑马程序员的《Java从入门到起飞》下部的43-63节,笔记包含方法引用和异常的相关用法及练习

文章目录
- 【Java学习|黑马笔记|Day19】
- 【DAY19】
- 一.方法引用
- 1)概述
- 2)引用静态方法
- 3.1)引用其他类的成员方法
- 3.2)引用本类或父类的成员方法
- 4)引用构造方法
- 5)类名引用成员方法
- 6)引用数组的构造方法
- 7)练习
- 7.1
- 7.2
- 二.异常
- 1)编译时异常和运行时异常
- 2)异常的作用
- 3)JVM虚拟机默认处理异常的方式
- 4)try...catch捕获异常
- 5)异常中的常见问题
- 6)抛出异常
- 7)综合练习
- 8)自定义异常
【DAY19】
一.方法引用
1)概述
把已经有的方法拿过来用,当做函数式接口中抽象方法的方法体
方法引用符:::
!!!注意

public class t1 {public static void main(String[] args) {//逆序排序Integer[] arr = {3,5,1,9,4,6,2,7};//匿名内部类Arrays.sort(arr,new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});//lambda表达式Arrays.sort(arr,(Integer o1,Integer o2) -> {return o2 -o1;});//方法引用Arrays.sort(arr,t1::subtraction);System.out.println(Arrays.toString(arr));}public static int subtraction(int a,int b){return b - a;}
}
分类
- 引用静态方法
- 引用成员方法
- 引用构造方法
2)引用静态方法
格式:类名::静态方法
eg:Integer::parsInt
//把集合中的元素都变成int类型
ArrayList<String> list = new ArrayList<>();
Collections.addAll(list, "1","2","3","4","5","6","7","8","9");list.stream().map(new Function<String, Integer>() {@Overridepublic Integer apply(String s) {int i = Integer.parseInt(s);return i;}
});//用方法引用简化
list.stream().map(Integer::parseInt).forEach(s -> System.out.println(s));
3.1)引用其他类的成员方法
格式:对象::成员方法
- 其他类:其他类对象::方法名
- 本类:this::方法名
- 父类:super::方法名
//需求:过滤数据只要a开头且三个字
ArrayList<String> list = new ArrayList<>();
Collections.addAll(list, "a", "b", "acd", "d", "aed");list.stream().filter(s -> s.startsWith("a")).filter(s ->s.length() == 3).forEach(s -> System.out.println(s));//创建函数式接口
list.stream().filter(new Predicate<String>() {@Overridepublic boolean test(String s) {return s.startsWith("a") && s.length() == 3;}
}).forEach(s -> System.out.println(s));//引用
list.stream().filter(new StringOperation()::stringJudge);
//为什么stringJudge不能是静态方法
//new StringOperation()::stringJudge:表示调用某个对象的实例方法
//所以,stringJudge 必须是:一个实例方法(不能是 static)并且可访问的(比如 public)
public class StringOperation {public boolean stringJudge(String s){return s.startsWith("a") && s.length() == 3;}
}
3.2)引用本类或父类的成员方法
- 本类:this::方法名
- 父类:super::方法名
引用处不能是静态方法
引用处是静态方法时需要new一个实例
public class t1 {public static void main(String[] args) {//需求:过滤数据只要a开头且三个字ArrayList<String> list = new ArrayList<>();Collections.addAll(list, "a", "b", "acd", "d", "aed");//引用本类中的方法//错误:list.stream().filter(this::stringJudge);//因为静态方法中没有thislist.stream().filter(new t1()::stringJudge).forEach(s -> System.out.println(s));}public boolean stringJudge(String s){return s.startsWith("a") && s.length() == 3;}}
4)引用构造方法
用来创建对象
格式:类名::new
范例:Student::new
public class t1{public static void main(String[] args) {//需求:集合里面存储姓名和年了吗,封装成Student对象并收集到List集合ArrayList<String> list = new ArrayList<>();Collections.addAll(list, "a,14", "b,15", "c,16", "d,17", "e,18", "f,19");List<Student> newList = list.stream().map(new Function<String, Student>() {@Overridepublic Student apply(String s) {String name = s.split(",")[0];int age = Integer.parseInt(s.split(",")[1]);return new Student(name, age);}}).collect(Collectors.toList());System.out.println(newList);//引用List<Student> newList2 = list.stream().map(Student::new).collect(Collectors.toList());System.out.println(newList2);}
}
public class Student {private String name;private int age;public Student() {}//再写一个构造方法public Student(String str){String name = str.split(",")[0];int age = Integer.parseInt(str.split(",")[1]);this.name = name;this.age = age;}public Student(String name, int age) {this.name = name;this.age = age;}//.......
}
5)类名引用成员方法
格式:类名::成员方法
eg:String::substring
规则:
-
需要有函数式接口
-
被引用的方法必须已经存在
-
被引用方法的形参需要跟抽象方法的第二个形参到最后一个形参保持一致,返回值必须保持一致
如果没有第二个参数,被引用方法必须是无参的
-
被引用方法的功能必须满足需求
public class t1{public static void main(String[] args) {//需求:集合里面的字符串变成大写后进行输出ArrayList<String> list = new ArrayList<>();Collections.addAll(list, "a", "b", "c","d","e","f","g");list.stream().map(new Function<String, String>() {//抽象方法第一个参数://表示被引用方法的调用着,决定了可以引用哪些类中的方法,//eg:此处第一个参数是String类型的只能调用String类中的方法,比如toUpperCase@Overridepublic String apply(String s) {return s.toUpperCase();}}).forEach(s -> System.out.println(s));//方法引用//拿着流里面的每一个数据去调用String类中的toUpperCase方法,方法返回值就是转换后的结果list.stream().map(String::toUpperCase).forEach(s -> System.out.println(s));}
}
6)引用数组的构造方法
格式:数据类型[]::new
eg:int[]::new
public class t1{public static void main(String[] args) {//需求:集合中存储一些整数,收集到数组中ArrayList<Integer> list = new ArrayList<>();Collections.addAll(list,1,2,3,4,5,6,7,8,9,10);Integer[] arr = list.stream().toArray(new IntFunction<Integer[]>() {@Overridepublic Integer[] apply(int value) {return new Integer[value];}});System.out.println(Arrays.toString(arr));//细节:数组的类型需要跟流中数据的类型保持一致Integer[] arr2 = list.stream().toArray(Integer[]::new);//Ctrl + Alt + V自动生成左边变量System.out.println(Arrays.toString(arr2));}
}
7)练习
7.1
集合中存储一些字符串数据,收集到Student类型的数组中
//练习一
ArrayList<String> list = new ArrayList<>();
Collections.addAll(list,"a,14","b,23","c,16","d,31");Student[] arr = list.stream().map(Student::new).toArray(Student[]::new);System.out.println(Arrays.toString(arr));
7.2
创建集合添加学生对象,获取姓名并存放到数组中
public class t1{public static void main(String[] args) {//练习二ArrayList<Student> list = new ArrayList<>();list.add(new Student("a",18));list.add(new Student("b",19));list.add(new Student("c",20));list.add(new Student("d",21));list.add(new Student("e",22));String[] arr = list.stream().map(new Function<Student,String>() {@Overridepublic Strin g apply(Student student) {return student.getName();}}).toArray(String[]::new);String[] arr2 = list.stream().map(Student::getName).toArray(String[]::new);System.out.println(Arrays.toString(arr2));}
}
技巧
- 现在有没有一个方法符合的当前的需求
- 如果有是否满足引用的规则
二.异常
异常:异常就是程序出现的问题
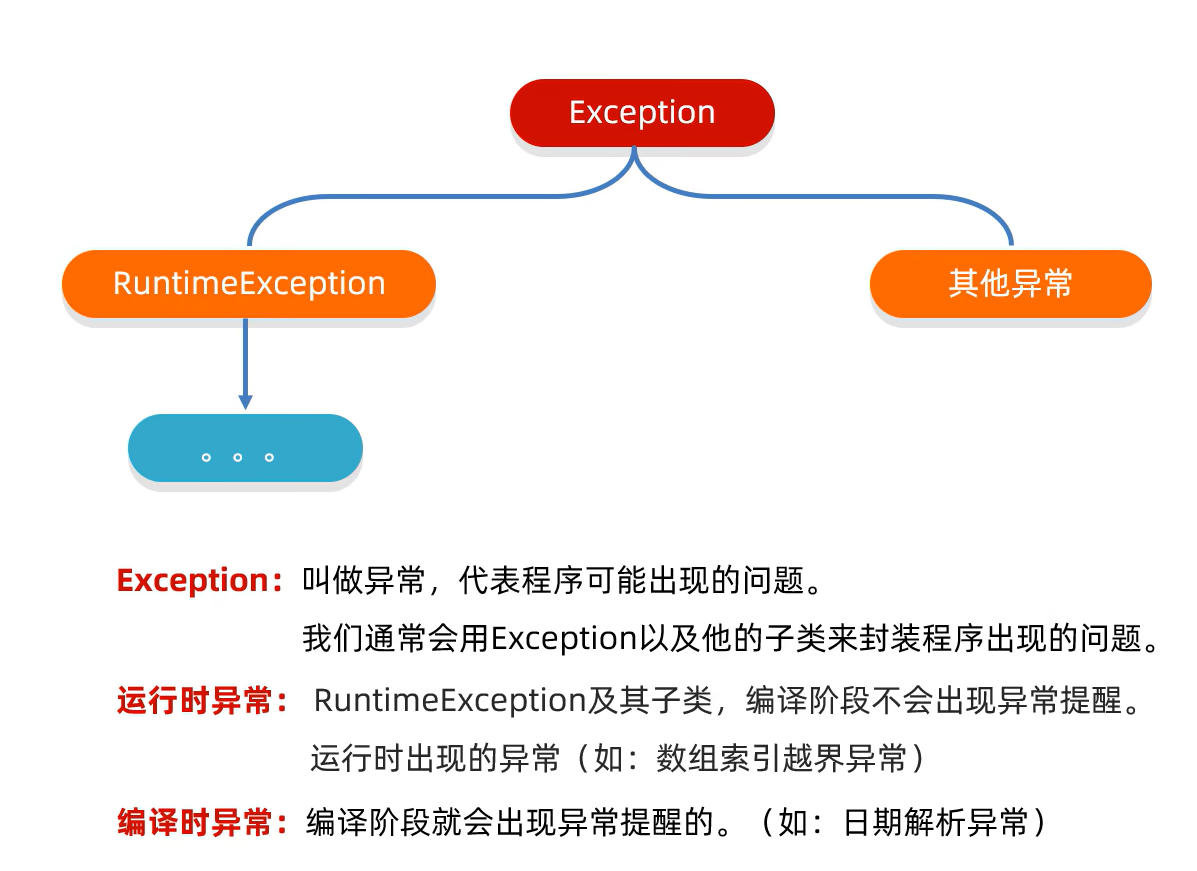
1)编译时异常和运行时异常
编译时异常:要手动处理,否则代码报错(如日期解析异常)
运行时异常:在代码运行时出现的异常 (如数组索引越界异常)

2)异常的作用
一:异常是用来查询不管的关键参考信息
二:异常可以作为方法内部的一种特殊返回值,以便通知调用者底层的执行情况
3)JVM虚拟机默认处理异常的方式
- 把异常的名称,异常的原因及异常出现的位置灯信息输出在控制台上
- 程序停止执行,下面的代码不会再执行了
4)try…catch捕获异常
格式:
try{可能出现异常的代码
}catch{异常的处理代码
}
目的:当代码出现异常时,可以让程序继续执行下去
eg
int[] arr = {1,2,3,4,5,6};try{//可能出现异常的代码System.out.println(arr[10]);//此处出现了异常,程序就会在这创建一个ArrayIndexOutOfBoundsException对象//new ArrayIndexOutOfBoundsException();//拿着这个对象和catch小括号对比,看小括号中的变量是否能接收这个对象//如果能被接受表示该异常被捕获了,执行catch里面的代码
}catch(ArrayIndexOutOfBoundsException e){//如果出现ArrayIndexOutOfBoundsException异常该如何处理System.out.println("索引越界了");
}
System.out.println("看看我执行了吗");
//好处:可以让程序继续执行不会停止
如果try中没有遇到问题:不执行catch里面的代码
如果try中遇到多个问题:要写多个catch与之对应
int[] arr = {1,2,3,4,5,6};
try{System.out.println(arr[10]);System.out.println(2/0);
}catch(ArrayIndexOutOfBoundsException e){System.out.println("索引越界");
}catch(ArithmeticException e){System.out.println("除数不能为0");
}catch(Exception e){//父类一定要写在下面 因为遇到异常匹配catch时是从上到下依次System.out.println("异常");
}
System.out.println("看看我执行了吗");
int[] arr = {1,2,3,4,5,6};
try{System.out.println(arr[10]);System.out.println(2/0);
}catch(ArrayIndexOutOfBoundsException | ArithmeticException e){System.out.println("索引越界");
}//JDK8以后一个catch可以捕获多个异常中间用|隔开 表示几个异常可以用同一种解决方法
System.out.println("看看我执行了吗");
如果try中遇到的异常没有被捕获:相当于try…catch白写了 最终还是交给虚拟机处理
如果try中遇到问题:try下面的其他代码将不会执行,直接跳转catch
5)异常中的常见问题
Throwable的成员方法
| 方法名称 | 说明 |
|---|---|
| public String getMessage() | 返回此throwable的详细消息字符串 |
| public String toString() | 返回此可抛出的简短描述 |
| public void printfStackTrace() | 把异常的错误信息输出在控制台 |
int[] arr = {1,2,3,4,5,6};
try {System.out.println(arr[10]);//生成try...catch快捷键 Ctrl + Alt + T
} catch (ArrayIndexOutOfBoundsException e) {System.out.println(e.getMessage());//Index 10 out of bounds for length 6
}System.out.println("看看我执行了吗");
int[] arr = {1,2,3,4,5,6};
try {System.out.println(arr[10]);//生成try...catch快捷键 Ctrl + Alt + T
} catch (ArrayIndexOutOfBoundsException e) {System.out.println(e.toString());//java.lang.ArrayIndexOutOfBoundsException: Index 10 out of bounds for length 6
}System.out.println("看看我执行了吗");
int[] arr = {1,2,3,4,5,6};
try {System.out.println(arr[10]);//生成try...catch快捷键 Ctrl + Alt + T
} catch (ArrayIndexOutOfBoundsException e) {e.printStackTrace();//仅仅是打印信息不会停止运行
}System.out.println("看看我执行了吗");
拓
System.out.println(123);
System.err.println(123);//用来打印错误的输出语句 打印在控制台上是红色的字
6)抛出异常
throws
写在方法定义处,表示声明一个异常,告诉调用者使用本方法可能会有哪些异常
public void 方法()throws 异常类名1,异常类名2...{...
}
编译时异常:必须写
运行时异常:可以不写
throw
写在方法内,结束方法
手动抛出异常对象交给调用者
方法中下面的代码不再执行了
public void 方法(){throw new NullPointerException();
}
eg:
public class t1{public static void main(String[] args) {//定义一个方法求最大值int[] arr = null;int max = 0;try {max = getMax(arr);} catch (NullPointerException e) {System.out.println("空指针异常");} catch (ArrayIndexOutOfBoundsException e) {System.out.println("索引越界异常");}System.out.println(max);}public static int getMax(int[] arr) throws NullPointerException,ArrayIndexOutOfBoundsException {if (arr == null) {//手动创建一个异常对象,并把这个异常交给方法的调用者处理//此时方法就会结束,下面的代码不会执行了throw new NullPointerException();}if(arr.length == 0){throw new ArrayIndexOutOfBoundsException();}int max = arr[0];for (int i = 0; i < arr.length; i++) {if(arr[i] > max){max = arr[i];}}return max;}
}

7)综合练习
抛出:告诉调用者出错了
捕获:不让程序停止
public class t1{public static void main(String[] args) {//键盘录入男朋友姓名和年龄//年龄在18 - 30之间//姓名在3 - 10个字//超出范围是异常数据不能复制,需要重新录入直到正确为止Scanner sc = new Scanner(System.in);BoyFriend bf = new BoyFriend();while (true) {try {System.out.println("请输入名字");String name = sc.nextLine();bf.setName(name);System.out.println("请输入年龄");String agestr = sc.nextLine();int age = Integer.parseInt(agestr);bf.setAge(age);//如果所有的数据都正确跳出循环break;}catch (NumberFormatException e) {System.out.println("年龄格式有误,请输入数字");}catch (RuntimeException e){System.out.println("姓名的长度或年龄范围有误");}}System.out.println(bf);}
}
public class BoyFriend {private String name;private int age;//......public void setName(String name) {int len = name.length();if(len < 3 || len > 10) {throw new RuntimeException();}this.name = name;}public void setAge(int age) {if(age < 18 || age >30){throw new RuntimeException();}this.age = age;}//......
}
8)自定义异常
步骤:
- 定义异常类
- 写继承关系
- 空参构造
- 带参构造
意义:为了让控制台的报错信息更加见名知意
例:优化上题代码
1.创建自定义异常
public class NameFormatException extends RuntimeException {//姓名格式化问题//运行时:表示由于参数错误而导致的问题//编译时:提醒程序员检查本地信息public NameFormatException() {}public NameFormatException(String message) {super(message);}
}
public class AgeOutOfBoundsException extends RuntimeException {//年龄越界错误public AgeOutOfBoundsException() {}public AgeOutOfBoundsException(String message) {super(message);}
}
2.修改BoyFriend类中的方法
//........public void setName(String name) {int len = name.length();if(len < 3 || len > 10) {throw new NameFormatException(name + "格式有误");}this.name = name;
}public void setAge(int age) {if(age < 18 || age >30){throw new AgeOutOfBoundsException(age + "年龄越界");}this.age = age;
}//.........
3.修改try…catch
public class t1{public static void main(String[] args) {//键盘录入男朋友姓名和年龄//年龄在18 - 30之间//姓名在3 - 10个字//超出范围是异常数据不能复制,需要重新录入直到正确为止Scanner sc = new Scanner(System.in);BoyFriend bf = new BoyFriend();while (true) {try {System.out.println("请输入名字");String name = sc.nextLine();bf.setName(name);System.out.println("请输入年龄");String agestr = sc.nextLine();int age = Integer.parseInt(agestr);bf.setAge(age);//如果所有的数据都正确跳出循环break;}catch (NumberFormatException e) {e.printStackTrace();}catch (NameFormatException e){e.printStackTrace();}catch(AgeOutOfBoundsException e){e.printStackTrace();}}System.out.println(bf);}
}
(笔记内容主要基于黑马程序员的课程讲解,旨在加深理解和便于日后复习)

希望这篇笔记能对大家的学习有所帮助,有啥不对的地方欢迎大佬们在评论区
